2016年四川高考文科数学试题解析(word版
2016年高考四川文科数学
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1.设i为虚数单位,则复数(1+i)2=
(A) 0
(B)2
(C)2i
(D)2+2i
【答案】C
【解析】
 (A)6 (B) 5 (C)4(D)3
(A)6 (B) 5 (C)4(D)3
【答案】B

考点:集合中交集的运算.
3.抛物线y2=4x的焦点坐标是
(A)(0,2)
(B) (0,1)
(C) (2,0)
(D) (1,0)
【答案】D
【解析】
 【答案】A
【答案】A
【解析】
![]() 故选A.
故选A.
考点:三角函数图像的平移.
5.设p:实数x,y满足x>1且y>1,q: 实数x,y满足x+y>2,则p是q的
(A)充分不必要条件 (B)必要不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
【答案】A
【解析】
![]() 充分不必要条件,选A.
充分不必要条件,选A.
考点:充分必要条件.
6.已知a函数f(x)=x3-12x的极小值点,则a=
(A)-4 (B) -2 (C)4 (D)2
【答案】D
 考点:函数导数与极值.
考点:函数导数与极值.
7.某公司为激励创新,计划逐年加大研发奖金投入。若该公司2015年全年投入研发奖金130万元,在此基础上,每年投入的研发奖金比上一年增长12%,则该公司全年投入的研发奖金开始超过200万元的年份是
(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30) www.gaosan.com
(A)2018年(B)2019年(C)2020年(D)2021年
【答案】B
【解析】
试题分析:设从2015年后第n年该公司全年投入的研发资金开始超过200万元,由已知得 考点:1.增长率问题;2.常用对数的应用.
考点:1.增长率问题;2.常用对数的应用.
8.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法。如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为
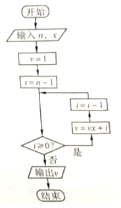
(A)35(B)20(C)18(D)9
【答案】C
考点:1.程序与框图;2.秦九韶算法;3.中国古代数学史. www.gaosan.com
 【答案】B
【答案】B

考点:1.向量的数量积运算;2.向量的夹角;3.解析几何中与圆有关的最值问题.

考点:三角函数诱导公式
已知某三菱锥的三视图如图所示,则该三菱锥的体积 。www.gaosan.com
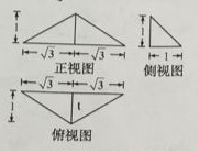
![]()

考点:1.三视图;2.几何体的体积.
从2、3、8、9任取两个不同的数值,分别记为a、b,则![]() 为整数的概率= 。
为整数的概率= 。
【答案】1/6
【解析】
 时,定义“伴随点”为它自身,现有下列命题:
时,定义“伴随点”为它自身,现有下列命题:
若点A的“伴随点”是点![]() ,则点
,则点![]() 的“伴随点”是点A.
的“伴随点”是点A.
单元圆上的“伴随点”还在单位圆上。
若两点关于x轴对称,则他们的“伴随点”关于y轴对称
④若三点在同一条直线上,则他们的“伴随点”一定共线。
其中的真命题是 。
【答案】②③

考点:1.新定义问题;2.曲线与方程.
16、(12分)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图。
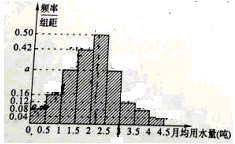
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数。
【答案】(Ⅰ)a=0.3;(Ⅱ)36000;(Ⅲ)2.04.

考点:频率分布直方图、频率、频数的计算公式
17、(12分)
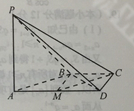
如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=½AD。
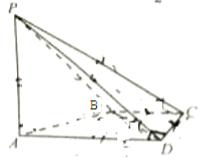
(I)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;www.gaosan.com
(II)证明:平面PAB⊥平面PBD。
【答案】(1)取棱AD的中点M,证明详见解析;(2)证明详见解析.
【解析】
试题分析:本题考查线面平行、线线平行、线线垂直、线面垂直等基础知识,考查空间想象能力、分析问题的能力、计算能力.第一问,利用线面平行的定理,先证明线线平行,再证明线面平行;第二问,先由线面垂直得到线线垂直,在利用线面垂直的性质得到BD⊥平面PAB,最后利用面面垂直的判定定理证明面面垂直.
试题解析:


考点:线面平行、线线平行、线线垂直、线面垂直.
18、(本题满分12分)
 【答案】(1)证明详见解析;(2)4.
【答案】(1)证明详见解析;(2)4.
【解析】
试题分析:本题考查正弦定理、余弦定理、商数关系等基础知识,考查学生的分析问题的能力和计算能力.第一问,利用正弦定理,将边角进行转化,结合诱导公式进行证明;第二问,利用余弦定理解出cos A=3/5,再根据平方关系解出sinA,代入已知中,解出tanB的值.
 考点:正弦定理、余弦定理、商数关系
考点:正弦定理、余弦定理、商数关系
19、(本小题满分12分)
已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=Sn+1,其中q﹥0,n∈N+
(Ⅰ)若a2,a3,a2+ a3成等差数列,求数列{an}的通项公式;


 考点:数列的通项公式、双曲线的离心率、等比数列的求和公式
考点:数列的通项公式、双曲线的离心率、等比数列的求和公式
20、(本小题满分13分)



考点:椭圆的标准方程及其几何性质.
21、(本小题满分14分)

















